LDA实作指南
LDA的动机和思路
让我们从下面这张图讲起:
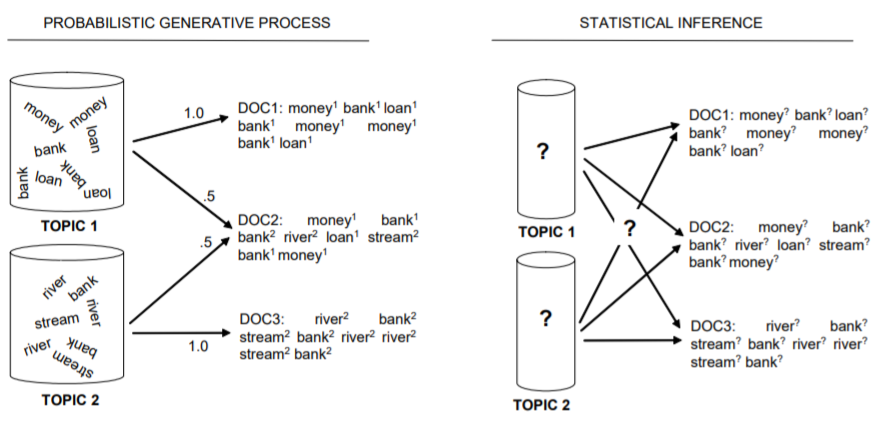
生成过程是按照一定的概率选择topic,再从对应topic中按照一定概率选择token;而推断过程则是给定了一些文档和其中的token,不知道每个token是由哪个topic生成,需要去推断每篇文档取自各个主题的概率,以及每个主题在抽出各个词的概率。
这个推断不能胡乱推断,而应该根据一定的假设进行,这个假设就是LDA的生成过程(这也是为什么许多介绍LDA的文章会在一开始就把LDA的生成过程写出来)。
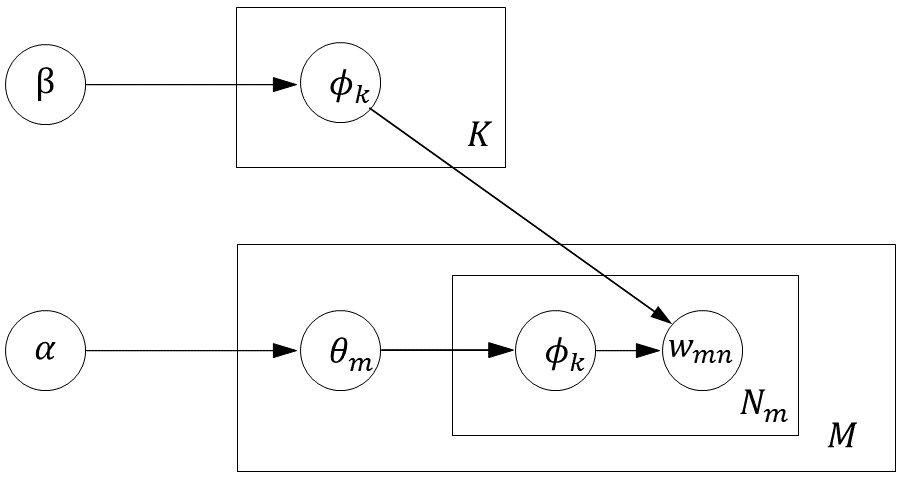
根据上述生成过程,我们可以看出,其中最重要的就是给出参数$\Theta$和$\Phi$的估计,也就是$\theta_{m}$和$\phi_{k}$的估计。这两个参数的估计都可以通过主题分配向量$\textbf{z}$的采样来得到,也就是说,如果能够“合理”地给出每个词的主题分配情况(即$\textbf{z}$的若干采样),那么就能推断出$\theta$和$\phi$。
于是问题就变成,在给定观测数据$\textbf{w}$和先验超参数$\alpha$和$\beta$的前提下,如何推断$\textbf{z}$的分布(进而可以从中采样),也就是求:
$p(\textbf{z}|\textbf{w},\alpha,\beta)$,
由Bayes法则, $p(\textbf{z}|\textbf{w},\alpha,\beta)=\frac{p(\textbf{z},\textbf{w}|\alpha,\beta)}{p(\textbf{w}|\alpha,\beta)}$,分母由于维数过高极其稀疏而难以估计,注意到在对$\textbf{z}$的采样中,只需求得$\textbf{z}$在各主题上的相对概率大小即可,即$p(\textbf{z}|\textbf{w},\alpha,\beta)=\frac{p(\textbf{z},\textbf{w}|\alpha,\beta)}{p(\textbf{w}|\alpha,\beta)} \propto p(\textbf{z},\textbf{w}|\alpha,\beta)$,
因此现在关键在算$p(\textbf{z},\textbf{w}|\alpha,\beta)$,
根据生成过程,给定$\alpha$和$\beta$,要得到$\textbf{z}$和$\textbf{w}$,中间有隐变量$\theta$和$\phi$,因此上述条件概率需要将这两个隐变量通过积分消去(即求边缘概率),
$p(\textbf{z},\textbf{w}|\alpha,\beta)=\int{\int{p(\textbf{z},\textbf{w},\theta,\phi|\alpha,\beta) \mathrm{d}\theta} \mathrm{d}\phi} = \int{\int{p(\phi|\beta)p(\theta|\alpha)p(\textbf{z}|\theta)p(\textbf{w}|\phi_{z})\mathrm{d}\theta}\mathrm{d}\phi} = \int{p(\textbf{z}|\theta)p(\theta|\alpha)\mathrm{d}\theta}\int{p(\textbf{w}|\phi_{z})p(\phi|\beta)\mathrm{d}\phi}$,(也即=$p(\textbf{z}|\alpha)p(\textbf{w}|\textbf{z},\beta)$)
分别推导这两项:
记$\theta_{mk}$是第$m$个文本生成第$k$个主题的概率,$n_{mk}$是语料库中第$m$的文本生成第$k$个主题的次数,
第一项:
$$
\begin{align*}
p(\mathbf{z} \mid \alpha) &=
\int p(\mathbf{z} \mid \theta) p(\theta \mid \alpha) \mathrm{d} \theta \\
&=\int \prod_{m=1}^{M} \frac{1}{\mathrm{~B}(\alpha)} \prod_{k=1}^{K} \theta_{m k}^{n_{m k}+\alpha_{k}-1} \mathrm{~d} \theta \\
&=\prod_{m=1}^{M} \frac{1}{\mathrm{~B}(\alpha)} \int \prod_{k=1}^{K} \theta_{m k}^{n_{m k}+\alpha_{k}-1} \mathrm{~d} \theta \\
&=\prod_{m=1}^{M} \frac{\mathrm{B}\left(n_{m}+\alpha\right)}{\mathrm{B}(\alpha)} \\
\end{align*}
$$
,
(此处$p(\mathbf{z} \mid \theta) = \prod_{m=1}^{M} \prod_{k=1}^{K} \theta_{m k}^{n_{m k}}$,而由假设:$\theta$服从参数为$\alpha$的Dirichlet分布,因此$\theta$的先验分布$p(\theta \mid \alpha)=\frac{\Gamma\left(\sum_{i=1}^{k} \alpha_{i}\right)}{\prod_{i=1}^{k} \Gamma\left(\alpha_{i}\right)} \prod_{i=1}^{k} \theta_{i}^{\alpha_{i}-1}=\frac{1}{\mathrm{~B}(\alpha)} \prod_{i=1}^{k} \theta_{i}^{\alpha_{i}-1}=\operatorname{Dir}(\theta \mid \alpha)$,推导参考[1])。
第二项:
$$
\begin{align*}
p(\mathbf{w} \mid \mathbf{z}, \beta) &=\int p(\mathbf{w} \mid \mathbf{z}, \varphi) p(\varphi \mid \beta) \mathrm{d} \varphi \\
&=\int \prod_{k=1}^{K} \frac{1}{\mathrm{~B}(\beta)} \prod_{v=1}^{V} \varphi_{k v}^{n_{k v}+\beta_{v}-1} \mathrm{~d} \varphi \\
&=\prod_{k=1}^{K} \frac{1}{\mathrm{~B}(\beta)} \int \prod_{v=1}^{V} \varphi_{k v}^{n_{k v}+\beta_{v}-1} \mathrm{~d} \varphi \\
&=\prod_{k=1}^{K} \frac{\mathrm{B}\left(n_{k}+\beta\right)}{\mathrm{B}(\beta)}
\end{align*}
$$
,
其中$n_{k}=(n_{k1},n_{k2},\dots,n_{kV})$,(此处$p(\mathbf{w} \mid \mathbf{w}, \phi) = \prod_{k=1}^{K} \prod_{v=1}^{V} \phi_{kv}^{n_{kv}}$,同样由假设:$\phi$服从参数为$\beta$的Dirichlet分布,因此$\phi$的先验分布$p(\phi_{k} \mid \beta)=\frac{\Gamma\left(\sum_{i=1}^{V} \beta_{i}\right)}{\prod_{i=1}^{V} \Gamma\left(\beta_{i}\right)} \prod_{v=1}^{V} \phi_{kv}^{\beta_{v}-1}=\frac{1}{\mathrm{~B}(\beta)} \prod_{v=1}^{V} \phi_{kv}^{\beta_{v}-1}=\operatorname{Dir}(\phi \mid \beta))$)
可知:$p(\textbf{z},\textbf{w}|\alpha,\beta)=\prod_{d}\frac{B(n_{d,.}+\alpha)}{B(\alpha)} \prod_{k}\frac{B(n_{k,.}+\beta)}{B(\beta)}$,即$p(\textbf{z} |\textbf{w},\alpha,\beta) \propto \prod_{d}\frac{B(n_{d,.}+\alpha)}{B(\alpha)} \prod_{k}\frac{B(n_{k,.}+\beta)}{B(\beta)}$
于是我们可以据上式采样$p(\textbf{z}|\textbf{w},\alpha,\beta)$。直接采样是可以的,但高维空间效率极低,因此可以Gimbbs采样,一维一维地采,因此需要估计$p(z_{i}|\textbf{z}_{-i},\textbf{w},\alpha,\beta)$,易知:
$$
\begin{equation}
p(z_{i}|\textbf{z}{-i},\textbf{w},\alpha,\beta)
=\frac{p(z{i},\textbf{z}{-i}|\textbf{w},\alpha,\beta)}{p(\textbf{z}{-i}|\textbf{w},\alpha,\beta)}
=\frac{p(\textbf{z}|\textbf{w},\alpha,\beta)}{p(\textbf{z}_{-i}|\textbf{w},\alpha,\beta)}
\end{equation}
$$
,
分母 $p(\textbf{z}{-i},\textbf{w},\alpha,\beta)$ 记作$Z{i}$,$Z_{i}$为将位置$i$处的主题排除后的边缘概率,注意到$Z_{i}$与$z_{i}$的取值无关(因为$z_{i}$被排除了),即 $Z_{zi=t1}=Z_{zi=t2}(t1 \neq t2)$ ,因此
$p(z_{i}|\textbf{z}{-i},\textbf{w},\alpha,\beta)=\frac{p(\textbf{z}|\textbf{w},\alpha,\beta)}{Z{i}} \propto p(\textbf{z} | \textbf{w},\alpha,\beta) \propto \prod_{d}\frac{B(n_{d,.}+\alpha)}{B(\alpha)} \prod_{k}\frac{B(n_{k,.}+\beta)}{B(\beta)}$
即 $p(z_{i}|\textbf{z}{-i},\textbf{w},\alpha,\beta) \propto \frac{n{kv}+\beta_{v}}{\sum_{v=1}^{V}(n_{kv}+\beta_{v})} \frac{n_{mk}+\alpha_{k}}{\sum_{k=1}^{K}(n_{mk}+\alpha_{k})}$,(此步骤推断可参考文献[^2]P35)
到这里,LDA的Gibbs采样算法就呼之欲出了:
(以下摘自李航《统计学习方法》[^1])
-
Input:语料库的单词序列$\textbf{w}={\textbf{w}{1},\textbf{w}{2},\dots,\textbf{w}_{M}}$,
-
Output: 语料库的主题序列$\textbf{z}={\textbf{z}{1},\textbf{z}{2},\dots,\textbf{z}_{M}}$,估计模型参数$\theta$和$\phi$。
-
超参数:主题数$K$,Dirichlet参数$\alpha$和$\beta$。
-
初始化:
- “文档-主题”计数矩阵记为$C_{MK}$,其元素$C_{mk}$表示文档$m$中主题$k$的出现次数
- “主题-词”计数矩阵记为$P_{KV}$,其元素$P_{kv}$表示主题$k$中单词$v$的出现次数
- “文档-主题和”计数向量记为$(C_{1},C_{2},\dots,C_{M})$,其元素$C_{m}$表示文档$m$中包含的主题数
- “主题-词”计数向量记为$(P_{1},P_{2},\dots,P_{K})$,其元素$P_{k}$表示主题$k$中包含的单词数
以上变量均初始化为0,接着执行以下步骤:
对所有文档$\textbf{w}_{m}$:
对该文档中的所有单词$w_{mn},(n=1,2,\dots,N_{m})$:
基于多项分布抽样主题$z_{mn}=z_{k}\sim Mult(\frac{1}{K})$
$C_{mk} += 1$, $C_{m}+=1$, $P_{kv}+=1$, $P_{k}+=1$
-
学习:
对所有文档$\textbf{w}_{m}$:
对该文档中的所有单词$w_{mn}$:
设当前单词在词表中索引为$v$,所分配的主题$z_{mn}$的主题索引为$k$
$C_{mk} -= 1$, $C_{m}-=1$, $P_{kv}-=1$, $P_{k}-=1$
根据条件分布进行抽样:
$p(z_{i}|\textbf{z}{-i},\textbf{w},\alpha,\beta) \propto \frac{n{kv}+\beta_{v}}{\sum_{v=1}^{V}(n_{kv}+\beta_{v})} \frac{n_{mk}+\alpha_{k}}{\sum_{k=1}^{K}(n_{mk}+\alpha_{k})}$,
设抽样得到主题$k^{\prime}$,令$z_{mn}=k^{\prime}$,
$C_{mk^{\prime}} += 1$, $C_{m}+=1$, $P_{k^{\prime}v}+=1$, $P_{k^{\prime}}+=1$
重复上述步骤,直至度过燃烧期,当收敛后,得到$\textbf{z}$的若干样本,于是可以据此估计参数$\theta$和$\phi$,注意是用分布的期望进行的估计,
最终得到$\theta_{mk}=\frac{n_{mk}+\alpha_{k}}{\sum_{k=1}^{K}(n_{mk}+\alpha_{k})}$,以及 $\phi_{kv}=\frac{n_{kv}+\beta_{v}}{\sum_{v=1}^{V}(n_{kv}+\beta_{v})}$。
算法完毕。
当有新文档来时,保留$\phi$,如上更新$\theta$,得到文档的主题分布。
估计参数$\theta$时,由LDA的定义,有
$p\left(\theta_{m} \mid \mathbf{z}{m}, \alpha\right)=\frac{1}{Z{\theta_{m}}} \prod_{n=1}^{N_{m}} p\left(z_{m n} \mid \theta_{m}\right) p\left(\theta_{m} \mid \alpha\right)=\operatorname{Dir}\left(\theta_{m} \mid n_{m}+\alpha\right)$,由Dirichlet分布的性质(参考[2]),得到
$\theta_{mk}=\frac{n_{mk}+\alpha_{k}}{\sum_{k=1}^{K}(n_{mk}+\alpha_{k})}$,
估计参数$\phi$时,有
$p\left(\varphi_{k} \mid \mathbf{w}, \mathbf{z}, \beta\right)=\frac{1}{Z_{\varphi_{k}}} \prod_{i=1}^{I} p\left(w_{i} \mid \varphi_{k}\right) p\left(\varphi_{k} \mid \beta\right)=\operatorname{Dir}\left(\varphi_{k} \mid n_{k}+\beta\right)$,同样由Dirichlet分布的性质,得到
$\phi_{kv}=\frac{n_{kv}+\beta_{v}}{\sum_{v=1}^{V}(n_{kv}+\beta_{v})}$
根据上述算法,可以很容易地写出程序,需要说明的是,本文的程序实现尽可能从易于理解的角度出发,并不打算作太多优化。这里以数据集作为示例数据。
首先进行分词,分词器选择HanLP;并去掉特殊符号和停用词,停用词表选用hit_stopwords。
1 | import re |
接下来实现LDA模型,我们希望实现如下接口:
1 | lda_model = LDA(docs=tokenized_docs,K=20) |
首先是初始化的部分,这部分可以很容易地完成,各关键部分的功能在注释中有所标注:
1 | class LDA: |
然后是LDA的训练部分:
1 | def train(self,n_iter=100): |
假如我们已经训练好了模型,后来又增加了新的训练数据,考虑添加一个add_docs接口,使模型在之前的基础上继续训练。在实现时可以有两种选择,一种是沿用之前的词表,只更新文档集,这样实现简单,计算效率也更高;另一种是扩充词表,这么做计算量会更大一些,但也更准确地反映了数据的变化。
1 | def add_docs(self,docs,n_iter=100): |
实现inference接口时,因为推断本质是加入新数据继续迭代至收敛,因此可复用已经实现的add_docs。剩下的接口都是辅助性功能,实现起来比较简单,就一并列出了。
1 | def batch_inference(self,docs,n_iter=100): |
让我们将模型应用到TNEWS上,迭代次数设定为100次,查看模型对文档主题分布$\theta$的推断,以及权重top20的主题词。
1 | if __name__ == '__main__': |
直观来说,从结果上看,部分主题的主题词具有一定关联性,而其余主题则较为隐晦;而定量地评测主题建模结果的优劣是另一个大话题,本文不予展开。如果我们更换一下停用词,比如把停用词换成baidu_stopwords,结果也会发生较大改变,这表明主题模型的效果受停用词库的影响较大,在选择停用词时应充分考虑数据所属的领域。