Implement LDA from scratch
Let’s start with the following figure:
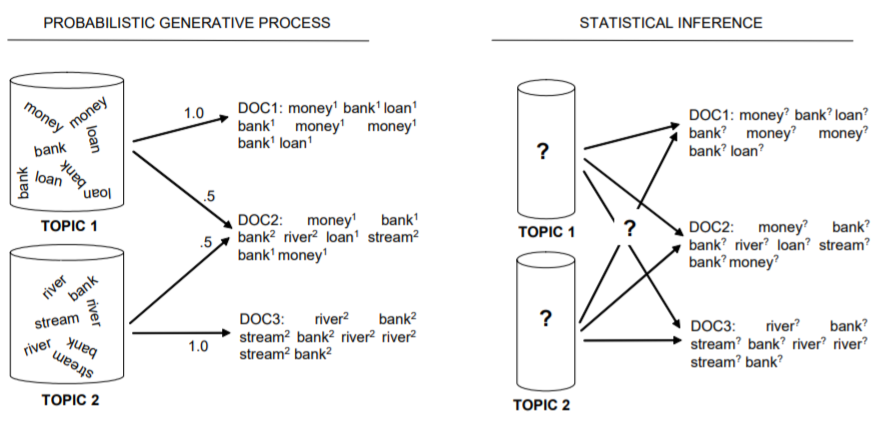
The generation process involves selecting a topic according to a certain probability, and then choosing a token from the corresponding topic based on a certain probability. In contrast, the inference process is given some documents and the tokens within them, but it is unknown which topic each token is generated from. The goal is to infer the probability that each document is derived from various topics, as well as the probability that each topic generates different words.
This inference should not be made arbitrarily, but should be based on certain assumptions. This assumption is the generation process of LDA (which is why many articles introducing LDA present the generation process at the very beginning).
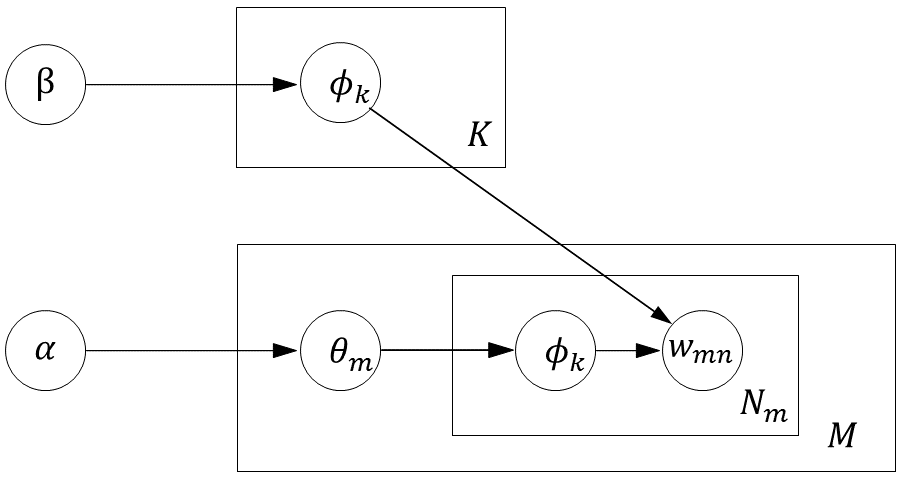
Based on the aforementioned generation process, it can be observed that the most critical aspect is to estimate the parameters $\Theta$ and $\Phi$, that is, the estimation of $\theta_{m}$ and $\phi_{k}$. The estimation of these two parameters can both be achieved through sampling of he topic assignment vector $\textbf{z}$. In other words, if one can “reasonably” provide the topic assignment for each word (i.e., several samples of $\textbf{z}$), then it is possible to infer $\theta$ and $\phi$.
Thus, the problem becomes how to infer the distribution of $\textbf{z}$
z
(and thereby sample from it) given the observed data
\textbf{w}
w
and the prior hyperparameters
\alpha
α
and
\beta
β
, which is to calculate:
p(\textbf{z}|\textbf{w},\alpha,\beta)
p(z|w,α,β)
.
By Bayes’ rule,
p(\textbf{z}|\textbf{w},\alpha,\beta)=\frac{p(\textbf{z},\textbf{w}|\alpha,\beta)}{p(\textbf{w}|\alpha,\beta)}
p(z|w,α,β)=p(z,w|α,β)p(w|α,β)
. The denominator is difficult to estimate due to its high dimensionality and extreme sparsity. It is noted that in the sampling of
\textbf{z}
z
, only the relative probability of
\textbf{z}
z
across different topics is required, that is,
p(\textbf{z}|\textbf{w},\alpha,\beta)=\frac{p(\textbf{z},\textbf{w}|\alpha,\beta)}{p(\textbf{w}|\alpha,\beta)} \propto p(\textbf{z},\textbf{w}|\alpha,\beta)
p(z|w,α,β)=p(z,w|α,β)p(w|α,β)∝p(z,w|α,β)
.
Therefore, the key now lies in calculating
p(\textbf{z},\textbf{w}|\alpha,\beta)
p(z,w|α,β)
.